Dưới đây là lời giải của một bạn bên mathlink, mọi người tham khảo thử! Xét trường hợp như hình vẽ dưới đây, các trường hợp khác chứng minh tương tự.
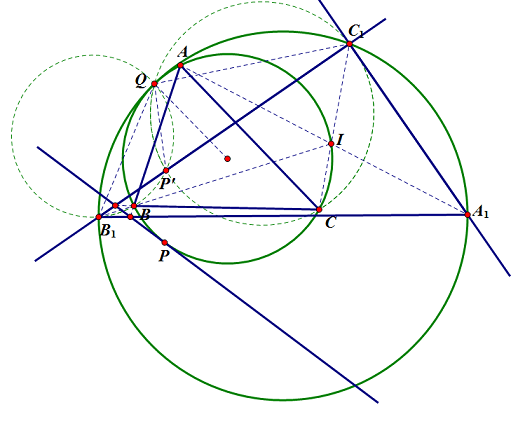
Gọi tam giác tạo thành bởi các đường thẳng $\l_a, \l_b, \l_c $ tương ứng là $A_1,B_1,C_1 $. Gọi P là tiếp điểm của đường thẳng $\l $ với $\Gamma $ và P' là điểm đối xứng với P qua BC. Dễ thấy P' thuộc $B_1C_1 $.
Trước hết, ta sẽ chứng minh rằng các đường thẳng $A_1A, B_1B, C_1C $ đồng quy tại một điểm nằm trên $\Gamma $.
Thật vậy, do $A_1C_1 $ đối xứng với $\l $ qua AC nên A cách đều hai đường thẳng $\l, A_1C_1 $, tuy nhiên do A cũng cách đều hai đường thẳng $\l, A_1B_1 $ nên A cách đều hai đường thẳng $A_1B_1, A_1C_1 $ hay $AA_1 $ là phân giác góc $\widehat{B_1A_1C_1} $.
Tương tự, ta cũng có $BB_1, CC_1 $ là các phân giác của tam giác $A_1B_1C_1 $. Suy ra các đường thẳng $AA_1, BB_1, CC_1 $ đồng quy, giả sử điểm đồng quy là I. Ta cần chứng minh I thuộc $\Gamma $.
Ta tính được $\widehat{B_1A_1C_1} = 180^0- 2\widehat{BAC} $ nên $\widehat{BIC} = \frac{1}{2}(\widehat{B_1} + \widehat{C_1}) = \widahat{BAC} $, tức là 4 điểm A, B, C, I cùng thuộc 1 đường tròn.
Gọi Q là giao điểm của $(BB_1P'), (CC_1P') $. Ta có:
$\widehat{BQP'} + \widehat{CQP'} = \widehat{BB_1P'}+\widehat{CC_1P'} = \widehat{BAC} $ nên bốn điểm A, B, C, Q cùng thuộc 1 đường tròn.
Ta cũng có:
$\widehat{B_1QC_1}= \widehat{B_1QB}+ \widehat{BQC}+ \widehat{CQC_1} = \widehat{B_1P'B}+\widehat{BAC}+\widehat{C_1P'C} = \widehat{BAC} + 180^0-\widehat{BPC}=2 \widehat{BAC} $. Suy ra bốn điểm $A_1, B_1, C_1, Q $ cùng thuộc 1 đường tròn.
Do đó, các đường tròn $\Gamma, (A_1B_1C_1) $ cắt nhau tại Q.
Cũng bằng biến đổi góc, ta thấy tiếp tuyến tại Q của $(\Gamma) $ trùng với tiếp tuyến tại Q của $(A_1B_1C_1) $ nên hai đường tròn này tiếp xúc với nhau tại Q. Ta có đpcm.
Bài này trông có nét giống bài IMO 2000 và có thể nói là hình vẽ cũng sáng sủa hơn.

[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT]