Một số kiến thức về hình trong các cuộc thi Olympic Toán !

[ma 29]

I.8)Một trường hợp đặc biệt của định lí Pappus qua góc nhìn hình xạ ảnh.


Ở phần này chúng tôi chỉ dùng hình xạ ảnh để dẫn dắt đến kết quả còn nội dung định lí và cách chứng minh thì hoàn toàn phù hợp với kiến thức hình THCS!
Ta có kết quả sau liên quan đến hình xạ ảnh: Các đường thẳng song song với nhau thì gặp nhau tại một điểm ở vô cực và ngược lại .
Vận dụng vào định lí Pappus ở trên , cho các điểm A,B,C ra vô cực thì theo kết quả về hình xạ ảnh ta có
YM//ZN ( Vì YM,ZN cùng đi qua một điểm (A) ở vô cực )Tương tự thì :XN//YP,XM//ZP.
Và khi ấy M,N,P vẫn thẳng hàng. Ta phát biểu lại được một định lí đơn giản và hữu dụng sau đây:


Định lí:Trên mặt phẳng cho ba điểm X,Y,Z thẳng hàng và ba điểm M,N,P thỏa mãn XN//YP,YM//ZN,XM//ZP.
Khi đó ta cũng có M,N,P thẳng hàng.

Chứng minh:

Trường hợp MP//XYZ thì đơn giản,bạn đọc tự chứng minh.
Ta sẽ xét khi MP không song song với XYZ.
Gọi S là giao điểm của MP với XYZ.
Đường thẳng qua X song song với YP cắt MP ở N'. Bài toán sẽ được gải quyết nếu ta chứng minh được rằng ZN' // YM (Vì khi ấy N' trùng N).

Thật vậy,chú ý YP//XN', ZP//XM nên theo Thales ta có:
$\frac{SY}{SZ} =\frac{SY}{SX} .\frac{SX}{SZ} = \frac{SP}{SN'} .\frac{SM}{SP} = \frac{SM}{SN'} $
Đến đây theo Thales đảo ta suy ra ZN' //YM. Chứng minh được hoàn tất.!
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[long14893]

I.9)Đẳng thức Ptolemy

Định lí Với tứ giác nội tiếp ABCD thì:
AB.CD+AD.BC=AC.BD

Chứng minh:

Lấy điểm E thuộc AC sao cho $\hat {DEC} =\hat {ADB} $

$\to \Delta ADB $đồng dạng $\Delta DEC \to \frac{AD}{DE} = \frac{DB}{DC}=\frac {AB}{EC} \to AB.DC = EC.DB $

Tương tự $\Delta ADE $đồng dạng $\Delta BDC \to AE.BD = AD.BC $$\to AD.BC+AB.CD = BD(EA+EC)=BD.AC (DPCM) $
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[ma 29]

I.13)Định lí Miquel

Định lí: Cho tam giác ABC và ba điểm M,N,P lần lượt nằm trên BC,CA,AB. Khi đó các đường tròn ngoại tiếp các tam giác APN,BPM và CMN đồng quy.

Chứng minh:

Gọi S là giao điểm của (BPM) và (CMN).Ta sẽ chứng minh S nằm trên (APN).
Thật vậy:

$(SN,SP) \equiv (SN,SM) + (SM,SP) \equiv (CN,CM) +(BM,BP) \equiv( CA,CB) + (BC,BA) \equiv (CA,BA) \equiv (AN,AP) (mod \pi) $

Suy ra điều cần chứng minh.!
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[nbkschool]

Hix vậy để em post cái khác đúng quy trình.:hugging:

I.16/Định lý Brokard

Định lý:
Cho tứ giác lồi ABCD nội tiếp đường tròn tâm O.AD giao BC tại M,AB giao CD tại N,AC giao BD tại I.Chứng minh rằng O là trực tâm của tam giác MIN.



Chứng minh:

Gọi H là giao thứ 2 của hai đường tròn ngoại tiếp các tam giác AID,BIC.
Xét tứ giác DOHC,ta có:
$\hat{DHC}=\360^o -\hat{DHI}-\hat{CHI}=\hat{DAC}+\hat{DBC}=\hat{DOC} $
Từ đó suy ra tứ giác DOHC nội tiếp.Tương tự ta cũng suy ra tứ giác AOHB nội tiếp.
Dễ thấy $\overline{NA}. \overline{NB}=\overline{NC}. \overline{ND} $ suy ra N nằm trên trục đẳng phương của hai đường tròn $(AIHD),(BIHC) $-->$O,H,N $ thẳng hàng.
Ta có:
$\hat{IHO}=\hat{IHD}-\hat{OHD}=\hat{ADC}+\hat{ACD}-\hat{OCD}=\hat{OCA}+\hat{ODA}+\hat{ODC} $
$=\90^o $
Từ đó suy ra $IM \perp ON $
Tương tự ta có:$IN \perp OM $
Suy ra O là trực tâm tam giác MIN (đpcm)

******T.Anh:Định lý này sử dụng cách chứng minh bằng cực đối cực sẽ nhanh hơn rất nhiều: Xem bài toán số 2 phần I mục C trong bài viết [Only registered and activated users can see links. ]
==============
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[trung anh]

I.17) Định lí Euler về khoảng cách giữa tâm 2 đường tròn nội, ngoại tiếp của tam giác



Định lý:
Cho tam giác ABC nội tiếp (O;R) và ngoại tiếp (I;r). Chứng minh rằng $OI^2=R^2-2Rr $.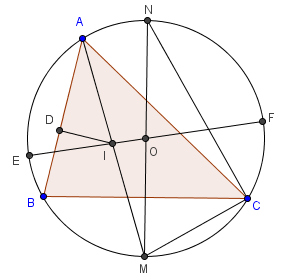

Chứng minh:
Kéo dài AI cắt (O) tại M. Vẽ đường kính MN của đường tròn (O).
Hạ $ID \perp AB $. Kéo dài OI cắt (O) tại E và F. Ta có $\Delta AID $ ~ $ \Delta NMC (g.g) \Rightarrow \frac{ID}{MC}=\frac{AI}{MN} \Rightarrow 2Rr=ID.MN=AI.MC $.
Mặt khác dễ dàng chứng minh $MC=MI \Rightarrow 2Rr=IA.IM $
Lại có $IA.IM=IE.IF=R^2-OI^2 $ nên ta có điều phải chứng minh.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[ma 29]

I.18)Định lí Euler về khoảng cách giữa tâm hai đường tròn nội ngoại tiếp tứ giác!(Định lí Fuss)

Định lí :Cho tứ giác ABCD vừa nội tiếp (O,R) vừa ngoại tiếp (I,r). Đặt d=OI. Khi đó ta có:

$\frac {1}{(R-d)^2} +\frac{1}{(R+d)^2} =\frac{1}{r^2}{ $


Chứng minh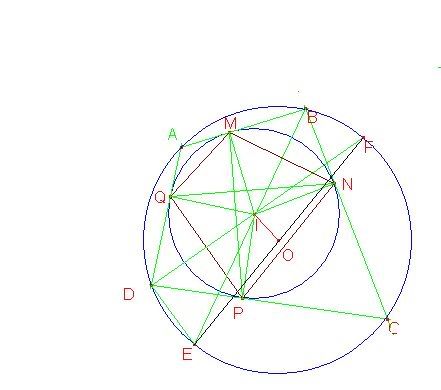


Gọi tiếp điểm của (I) trên AB,BC,CD,DA lần lượt là M,N,P,Q.
BI,CI cắt (O) lần lượt ở E,F .
Ta thấy:$(DE,DF) \equiv (DE,DC) +(DC,DF) \equiv (BE,BC) +(DC,DF) \equiv \frac{(BA,BC)+(DC,DA)}{2} \equiv \frac{\pi}{2} (mod \pi) $

Do đó E,O,F thẳng hàng ,nên O là trung điểm của EF.
Theo công thức đường trung tuyến trong tam giác IEF ta có:
$d^2 = IO^2 = \frac{IE^2}{2} + \frac{IF^2}{2} - \frac{EF^2}{4}=\frac{IE^2}{2} + \frac{IF^2}{2} -R^2 $
Từ đó suy ra:
$\frac {1}{(R-d)^2} +\frac{1}{(R+d)^2} = \frac{2(R^2+d^2)}{(R^2-d^2)^2} = \frac{IE^2 + IF^2} {(P_{I/(O)}) ^2} = \frac{IE^2}{(P_{I/(O)}) ^2} +\frac{IF^2}{ (P_{I/(O)}) ^2}= \frac{IE^2}{ (IE.IB)^2} +\frac{IF^2}{(IF.ID)^2} = \frac{1}{ IB^2} + \frac{1}{ ID^2} = \frac{1}{ ({\frac{IM}{ \sin{\frac{B}{2}}}) ^2 }}+ \frac{1}{(\frac{IP}{ (\sin {\frac{D}{2}}})^2} =\frac{1}{r^2} $ (vì$ \frac{B}{2}+ \frac{D}{2}=90) $
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[trung anh]

I.19)Định lí Casey(Định lí Ptolemy mở rộng)

Định lí :Cho tứ giác ABCD nội tiếp (O,R). Đặt các đường tròn $\alpha, \beta, \gamma, \delta $ là các đường tròn tiếp xúc với (O) tại các đỉnh A,B,C,D. Đăt $t_{\alpha\beta} $ là độ dài đoạn tiếp tuyến chung của hai đường tròn $\alpha, \beta $. Trong đó $t_{\alpha\beta} $ là độ dài tiếp tuyến chung ngoài nếu hai đường tròn $\alpha, \beta $ cùng tiếp xúc trong hoặc cùng tiếp xúc ngoài với (O), và là độ dài đoạn tiếp xúc trong nếu trong trường hợp còn lại. Các đoạn $t_{\beta\gamma}, t_{\gamma\delta} $, ... được xác định tương tự. Khi đó ta có:
$ t_{\alpha\beta}.t_{\gamma\delta}+t_{\beta\gamma}.t _{\alpha\delta}=t_{\alpha\gamma}.t_{\beta\delta} $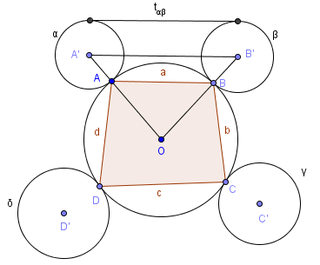



Chứng minh
Ta chứng minh trường hợp $\alpha, \beta, \gamma, \delta $ cùng tiếp xúc ngoài với (O). Các trường hợp còn lại chứng minh tương tự. Lần lượt đặt tâm các đường tròn trên là A',B',C',D' và bán kính lần lượt là x,y,z,t.
Đặt AB=a, BC=b, CD=c, DA=d, AC=m, BD=n.
Áp dụng định lý Pythagore:
$(t_{\alpha\beta})^2=A'B' ^2- (x-y)^2 $
Mặt khác lại có: (theo định lí hàm số cos)
$A'B' ^2=(R+x)^2+(R+y)^2-2(R+x)(R+y)cos(\hat{A'OB'}) $
$A'B' ^2=(R+x)^2+(R+y)^2-2(R+x)(R+y)(1-\frac{a^2}{2R^2}) $
$A'B' ^2=(R+x)^2-2(R+x)(R+y)+(R+y)^2+(R+x)(R+y).\frac{a^2}{R^2} $
$A'B' ^2=(x-y)^2+\frac{a^2}{R^2}.(R+x)(R+y) $
$\Rightarrow t_{\alpha\beta}=\frac{a}{R}.\sqrt{(R+x)(R+y)} $
Tương tự với $t_{\beta\gamma}, t_{\gamma\delta} $, ...
Ta có
$ t_{\alpha\beta}.t_{\gamma\delta}+t_{\beta\gamma}.t _{\alpha\delta}=t_{\alpha\gamma}.t_{\beta\delta} \Leftrightarrow a.c+b.d=m.n $(định lý Ptolemy)
Ngược lại ta thấy định lý Ptolemy là một trường hợp đặc biệt của định lí Casey khi x=y=z=t=0.
Xem [Only registered and activated users can see links. ]
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[trung anh]

I.20)Hệ thức Stewart

Định lí:Cho ba điểm A,B,C thẳng hàng. Và một điểm M bất kì. Ta luôn có hệ thức
$\bar{MA}^2.\bar{BC}+\bar{MB}^2.\bar{CA}+\bar{MC}^2 .\bar{AB}+\bar{BC}.\bar{CA}.\bar{AB}=0 $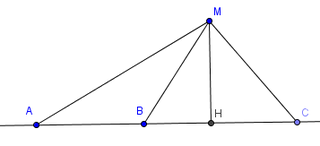



Chứng minh
Qua M hạ $MH \perp AC $.
Ta có:
$\bar{MA}^2.\bar{BC}+\bar{MB}^2.\bar{CA}+\bar{MC}^2 .\bar{AB}+\bar{BC}.\bar{CA}.\bar{AB} $
$=(MH^2+HA^2). \bar{BC}+(MH^2+HB^2).\bar{CA}+(MH^2+HC^2).\bar{AB} +\bar{BC}.\bar{CA}.\bar{AB} $
$=\bar{MH}^2.(\bar{BC}+\bar{CA}+\bar{AB})+(\bar{HA} ^2.\bar{BC}+\bar{HB}^2.\bar{CA}+\bar{HC}^2.\bar{AB }+\bar{BC}.\bar{CA}.\bar{AB}) $
$=0+\bar{HA}^2.\bar{BC}+\bar{HB}^2.\bar{CA}+\bar{HC }^2.\bar{AB}+\bar{BC}.\bar{CA}.\bar{AB} $
(Đưa về trường hợp hệ thức Stewart cho 4 điểm thẳng hàng (khi M nằm trên đường thẳng chứa A,B,C))
$\bar{HA}^2.\bar{BC}+\bar{HB}^2.\bar{CA}+\bar{HC}^2 .\bar{AB}+\bar{BC}.\bar{CA}.\bar{AB} $
$=\bar{HA}^2.( \bar{HC}-\bar{HB})+\bar{HB}^2.(\bar{HA}-\bar{HC})+\bar{HC}^2.(\bar{HB}-\bar{HA})+(\bar{HC}-\bar{HB}).(\bar{HA}-\bar{HC}).(\bar{HB}-\bar{HA})=0 $
Ta có đpcm.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[chu t tung]

I.21)Định lí Lyness
Định lí:Nếu đường tròn tâm O tiếp xúc trong với đường tròn ngoại tiếp tam giác ABC tại T và tiếp xúc với các cạnh AB,AC của tam giác lần lượt tại E và F thì tâm đường tròn nội tiếp của tam giác nằm trên EF.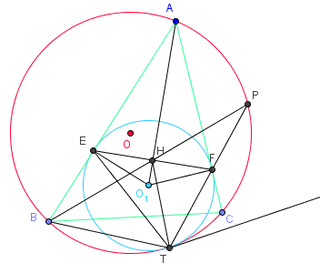

Chứng minh:
Để chứng minh định lí này ta cần chứng minh 2 bổ đề sau:
Bổ đề 1:AB là dây của một đường tròn tâm (O). Đường tròn (l) tiếp xúc với dây AB tại K và tiếp xúc trong với (O) tại T. Chứng minh L là trung điểm của cung AB ko chứa T và $LA^2=LK.LT $
Bổ đề 2: Điểm M là trung điểm cung BC ko chứa A của đường tròn ngoại tiếp tam giác ABC. Điểm I thuộc đoạn MA sao cho MI=MB. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác ABC.
Việc chứng minh 2 bổ đề này là khá đơn giản.
Ta tiếp tục quay trở lại với việc chứng minh định lí Lyness.
kẻ TF giao (O) tại P; BP cắt EF tại H.
Theo bổ đề 1 ta có BP là phân giác của góc B.
Ta có: $\hat{HET}=\hat{HBT} (=\hat{FTx}) \Rightarrow HEBT $ nt $\Rightarrow \hat{THB}=\hat{TEB} $
Mà $\hat{TEB}=\hat{TFE} \Rightarrow \hat{TFE}=\hat{THB} $
$\Rightarrow \Delta PHF \sim \Delta PTH \Rightarrow PH^2 = PF.PT $
Theo bổ đề 1 ta lại có $PC^2 = PF.PT \Rightarrow PC=PH $
Theo bổ đề 2 ta được H là tâm đường tròn nội tiếp tam giác ABC (ĐPCM)
Lần đầu vẽ hình xấu quá nhỉ!!!!!
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[nbkschool]

I.24)Công thức Jacobi liên quan đến tâm tỉ cự,định lí Lebnitz

1)Công thức Jacobi:

Nếu I là tâm tỉ cự của hệ điểm ${A_1,A_2,...,A_n} $ ứng với các hệ số $a_1,a_2,...,a_n $ thì với mọi điểm M trên mặt phẳng ta đều có:
$\sum^n_{i=1} a_iMA_i^2=\sum^n_{i=1}a_iIA_i^2+(a_1+...+a_n)MI^2 $

Chứng minh:

$\sum^n_{i=1} a_iMA_i^2=\sum^n_{i=1} a_i(\vec{MI}+\vec{IA_i})^2=(a_1+...+a_n)MI^2+2\vec {MI}( \sum^n_{i=1} a_i.\vec{IA_i})+\sum^n_{i=1} a_i.IA_i^2 $
$=(a_1+...+a_n)MI^2+\sum^n_{i=1}a_iIA_i^2 $
(do I là tâm tỉ cự của hệ điểm nên $\sum^n_{i=1} a_i.\vec{IA_i}=0 $)
->đpcm.

2)Định lí Lebnitz Đây là trường hợp đặc biệt của công thức trên khi n=3

3)Hệ quả khác:
Giá trị nhỏ nhất của biểu thức $\sum^n_{i=1} a_iMA_i^2 $ (với các kí hiệu như phần trên) đạt được khi $M \equiv I $.
(phần này thuần về tính toán nên chắc không cần vẽ hình phải không anh ma29?)
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[trung anh]

I.22)Định lý Lyness mở rộng(Bổ đề Sawayama)

Định lí:Cho tam giác ABC nội tiếp đường tròn (O).M thuộc BC (Có cách phát biểu khác là: cho tứ giác ABDC và M là giao của BC và AD; nhưng hai cách phát biểu này là tương đương). Một đường tròn (O') tiếp xúc với hai cạnh MA và MC tại E và F đồng thời tiếp xúc với cả đường tròn (O) tại K. Khi đó ta có tâm đường tròn nội tiếp của tam giác ABC nằm trên đường thẳng EF.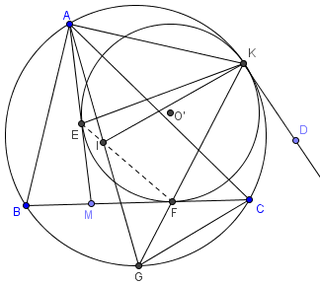



Chứng minh
KF cát đường tròn (O) tại G. Áp dụng bổ đề 1 tại bài viết của chu t tung về định lý Lyness ở trên, ta có G là điểm chính giữa cung BC. Gọi I là giao của AG với EF. Ta có
$\hat{IEK}=\hat{IAK}=\hat{FKD} \Rightarrow AEIK $ nội tiếp $\Rightarrow \hat{AIK} = \hat{EFK}=\hat{AEK} $
$\Rightarrow \Delta EFK $ ~ $\Delta IAK (g.g) \Rightarrow \hat{EKA}=\hat{GKI}=\hat{GIF} $
$\Rightarrow \Delta GIF $ ~ $\Delta GKI (g.g) \Rightarrow GI^2=GF.GK $
Lại cũng theo bổ đề 1 ta có $GC^2=GF.GK \Rightarrow GC=GI \Rightarrow $ I là tâm nội tiếp của $\Delta ABC $(theo bổ đề 2)
Xem thêm các hệ quả của định lý Lyness tại báo toán tuổi thơ 2 số 42 và 43
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[chu t tung]

I.23) Định lí Thébault
Định lí: Cho tam giác $ABC $ nội tiếp đường tròn $(O) $. $D $ là một điểm nằm trên cạnh $BC $. Đường tròn tâm $P $ tiếp xúc với 2 đoạn $AD,DC $ và tiếp xúc trong với $(O) $. Đường tròn tâm $Q $ tiếp xúc với 2 đoạn $AD,DB $ và tiếp xúc trong với $(O) $. Gọi $I $ là tâm nội tiếp tam giác $ABC $. Ta có: $P,I,Q $ thẳng hàng.
Chứng minh

Gọi $G,H $ lần lượt là tiếp điểm của $(Q) $ với $DB,AD $. Gọi $I $ là giao điểm của $EF $ và $GH $. Theo định lí lyness mở rộng(đã có trong bài của trung anh), $I $ là tâm nội tiếp tam giác $ABC $. Vậy ta chỉ cần chứng minh $P,I,Q $ thẳng hàng. Thật vậy, gọi $X,Y $ lần lượt là giao điểm của $GH $ và $DQ $; $EF $ và $DP $. Áp dụng định lí Thales ta có: $\frac{IX}{PD}=\frac{YD}{PD}=\frac{QX}{QD} $. Vậy , $P,I,Q $ thẳng hàng(dpcm)
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[BMW]

Nguyên văn bởi chu t tung

I.23) Định lí Thébault
Định lí: Cho tam giác $ABC $ nội tiếp đường tròn $(O) $. $D $ là một điểm nằm trên cạnh $BC $. Đường tròn tâm $P $ tiếp xúc với 2 đoạn $AD,DC $ và tiếp xúc trong với $(O) $. Đường tròn tâm $Q $ tiếp xúc với 2 đoạn $AD,DB $ và tiếp xúc trong với $(O) $. Gọi $I $ là tâm nội tiếp tam giác $ABC $. Ta có: $P,I,Q $ thẳng hàng.
Chứng minh

Gọi $G,H $ lần lượt là tiếp điểm của $(Q) $ với $DB,AD $. Gọi $I $ là giao điểm của $EF $ và $GH $. Theo định lí lyness mở rộng(đã có trong bài của trung anh), $I $ là tâm nội tiếp tam giác $ABC $. Vậy ta chỉ cần chứng minh $P,I,Q $ thẳng hàng. Thật vậy, gọi $X,Y $ lần lượt là giao điểm của $GH $ và $DQ $; $EF $ và $DP $. Áp dụng định lí Thales ta có: $\frac{IX}{PD}=\frac{YD}{PD}=\frac{QX}{QD} $. Vậy , $P,I,Q $ thẳng hàng(dpcm)

------------------------------


Chứng minh:$ \frac{IQ}{IP}=tan^{2}\frac{\widehat{ADC}}{2} $
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[avip]

Nguyên văn bởi BMW

------------------------------


Chứng minh:$ \frac{IQ}{IP}=tan^{2}\frac{\widehat{ADC}}{2} $

Phải là $\frac{IQ}{IP}=cot^{2}\frac{\widehat{ADC}}{2} $ mới đúng.
Ta có: $\frac{IQ}{IP} = \frac{YD}{YP} = \frac{YD/YE}{YP/YE} = \frac{\cot{\frac{ADC}{2}}}{\tan{\frac{ADC}{2}}} = \cot^2{\frac{ADC}{2}} $.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[ma 29]

Nguyên văn bởi chu t tung

Cứ tiến độ này chắc sang năm mới cái đống kiến thức hình này vẫn ko hoàn thành nổi mất thôi !!!!! Mọi người cố gắng đóng góp đi chứ:hornytoro:

Chú yên tâm ,sẽ xong trong năm nay! :hornytoro:
Nếu anh còn sống đến cuối năm thì anh cam đoan điều đó.!:nemoflow:
Mọi người cứ cố gắng nhá!!!:hornytoro:
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT]