Tiến tới kỳ thi Vietnam TST 2013

[namdung]

Chào các bạn,

Như vậy danh sách các thí sinh tham dự kỳ thi chọn đội tuyển toán dự IMO 2013 đã được xác định. Họ sẽ tiếp tục tranh tài với nhau để chọn ra 6 bạn có phong độ tốt nhất đại diện cho Việt Nam tại kỳ thi toán lớn nhất dành cho học sinh toàn thế giới.

Để chuẩn bị cho kỳ thi này, giúp các thí sinh có điều kiện làm quen với các bài toán "mức độ TST", cũng như thảo luận một số bài toán của các kỳ TST trước đó, bổ sung một số kiến thức và kỹ năng cần thiết cho các thí sinh, chúng tôi lập ra chủ đề này.

Chúng tôi sẽ lần lượt gửi lên các đề toán với nhiều mức độ: trung bình, tương đối khó, khó và rất khó thuộc về 4 phân môn: Đại số, Hình học, Số học và Tổ hợp. Chúng ta sẽ cùng giải, thảo luận, bình luận về cách giải, về phương pháp giải, về các kiến thức lý thuyết liên quan, và nêu các bài toán cùng dạng.

Chú ý rằng kinh nghiệm của các kỳ TST trước cho thấy, để lọt vào đội tuyển thì phải làm được các bài trung bình và tương đối khó một cách hoàn hảo và kiếm điểm được ở những bài khó, trong đó vế đầu gần như là điều kiện tiên quyết. Vì thế các bạn cũng chú ý giải cẩn thận và chi tiết những bài thuộc loại trung bình và cũng đừng quá hoang mang khi thấy một số bài gần như "ngoài vùng phủ sóng" của các bạn.

Chúng ta bắt đầu từ 4 bài toán đầu tiên (làm trong 450 phút):

1. Cho 0 < a, b, c, d < 1 và abcd = (1-a)(1-b)(1-c)(1-d). Chứng minh rằng
$ (a+b+c+d) - (a+c)(b+d) \ge 1 $

2. Chứng minh rằng với mọi số nguyên dương n > 1 tổng $1^{1} + {3}^{3} + {5}^{5} + ... + {(2^n-1)^{2^n-1} $ chia hết cho $2^n $ nhưng không chia hết cho $2^{n+1} $

3. Cho tam giác nhọn ABC. M, N là trung điểm các cạnh AB, AC tương ứng và gọn P là hình chiếu của N lên cạnh BC và $A_1 $ là trung điểm của MP. Các điểm $B_1, C_1 $ được xây dựng một cách tương tự. Chứng minh rằng nếu $AA_1, BB_1, CC_1 $ đồng quy tại một điểm thì tam giác ABC cân.

4. Một đường tròn màu xanh được chia bởi 100 điểm màu đỏ thành các cung có độ dài theo một thứ tự tùy ý nào đó là 1, 2, ..., 100. Chứng minh rằng tồn tại một đường kính có hai đầu mút màu đỏ.

Chủ đề mong nhận được sự ủng hộ và chung tay của các thầy giáo, các cựu IMO, cựu TST, cựu VMO để cùng hướng dẫn, chia sẻ kinh nghiệm.

Chú ý khi post đề bài lên cần cân nhắc và chọn lọc kỹ càng, với mỗi bài toán nên gắn liền với một phương pháp, một kỹ thuật cụ thể mà các bạn muốn truyền đến cho các bạn thí sinh. Gọi là Quý hồ tinh bất quý hồ đa.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[huynhcongbang]

Em xin giải bài 3.

Bài này cũng xuất hiện trong khá nhiều tài liệu, thuộc về nội dung hình học tính toán. Lúc trước em có phát biểu lại một tí nhưng vấn đề cơ bản thì vẫn thế. Dưới đây là lời giải chi tiết.

Cho tam giác $ABC$ nhọn, không cân có diện tích S và có $M, N$ lần lượt là trung điểm $AB, AC.$ Với $x\in \left( 0;1 \right)$, xét điểm $M, N$ lần lượt thuộc các cạnh $AB, AC$ sao cho $\frac{AM}{AB}=\frac{AN}{AC}=x$ và gọi $X$ tâm của hình chữ nhật ${{R}_{1}}$ nội tiếp tam giác $ABC$ với $M, N$ là hai đỉnh của hình chữ nhật ${{R}_{1}}$ và hai đỉnh còn lại thuộc cạnh $BC$. Ứng với hai số thực $y,z\in \left( 0;1 \right)$, ta lần lượt xét các hình chữ nhật ${{R}_{2}},{{R}_{3}}$ với tâm của chúng theo thứ tự là $Y$ và $Z$ với cách xác định tương tự.
a) Chứng minh rằng ${{S}_{{{R}_{1}}}}{{S}_{{{R}_{2}}}}{{S}_{{{R}_{3}} }}\le \frac{1}{8}S^3$.
b) Trong trường hợp dấu đẳng thức xảy ra trong bất đẳng thức trên, chứng minh rằng các đường thẳng $AX, BY, CZ$ không đồng quy.

Lời giải.

a) Giả sử hình chữ nhật tương ứng có tâm $X$ là $MNPQ$ với $P, Q$ thuộc cạnh $BC$.
Theo định lí Thales thì:

$\frac{MN}{BC}=\frac{AM}{AB}=x$ và $\frac{MQ}{AH}=\frac{BM}{AB}=1-\frac{AM}{AB}=1-x$

trong đó $H$ là hình chiếu của $A$ lên cạnh $BC$.
Suy ra ${{S}_{MNPQ}}=MN.MQ=x(1-x).AH.BC=2x(1-x)S$.
Theo bất đẳng thức Cauchy cho hai số không âm $x,1-x$ thì $x(1-x)\le \frac{{{(x+1-x)}^{2}}}{4}=\frac{1}{4}$ nên ta có ${{S}_{{{R}_{1}}}}=2x(1-x)S\le \frac{1}{2}S$.
Tương tự, ta cũng có ${{S}_{{{R}_{2}}}}\le \frac{1}{2}S,{{S}_{{{R}_{3}}}}\le \frac{1}{2}S$. Nhân các bất đẳng thức này lại, ta được đpcm.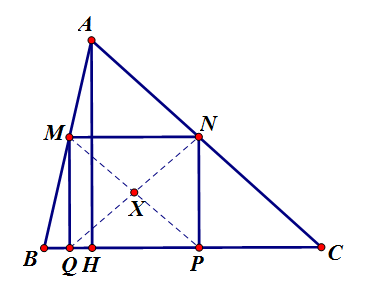

b) Dễ thấy rằng dấu bằng xảy ra trong các bất đẳng thức trên khi và chỉ khi $x=y=z=\frac{1}{2}$ hay cứ mỗi hình chữ nhật thì có một cạnh là đường trung bình của tam giác ABC.
Ta sẽ tính tỉ lệ $\dfrac{\sin \angle XAB}{\sin \angle XAC}$ theo độ dài các cạnh của tam giác $ABC$. Đặt $BC=a,CA=b,AB=c.$
Ta có $$\frac{{{S}_{AMX}}}{{{S}_{ANX}}}=\frac{AM.AX.\sin \angle XAB}{AN.AX.\sin \angle XAC}\Rightarrow \frac{\sin \angle XAB}{\sin \angle XAB}=\frac{{{S}_{AMX}}}{{{S}_{ANX}}}\frac{b}{c}. $$ Hơn nữa, theo tỉ lệ diện tích các tam giác, ta có $${{S}_{AMX}}=\frac{1}{2}{{S}_{AMP}}=\frac{1}{4}{{ S}_{ABP}}=\frac{BP}{BC}S=\frac{a-\frac{b}{2}\cos C}{4a}S=\frac{a-\frac{b}{2}\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}}{4a}S=\frac{3{{a}^{2}}-{{b}^{2}}+{{c}^{2}}}{16{{a}^{2}}}S. $$
Tương tự, ta cũng tính được

${{S}_{ANX}}=\dfrac{3{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{16{{a}^{2}}}S$ nên $\dfrac{\sin \angle XAB}{\sin \angle XAC}=\dfrac{3{{a}^{2}}-{{b}^{2}}+{{c}^{2}}}{3{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}\cdot \frac{b}{c}$.

Xây dựng các đẳng thức tương ứng về góc đối với Y và Z rồi áp dụng định lí Ceva, ta thấy điều kiện để các đoạn $AX, BY, CZ$ đồng quy khi và chỉ khi $$\prod\limits_{sym}{\left( \frac{3{{a}^{2}}-{{b}^{2}}+{{c}^{2}}}{3{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}\cdot \frac{b}{c} \right)}=1\Rightarrow \prod\limits_{sym}{\left( \frac{3{{a}^{2}}-{{b}^{2}}+{{c}^{2}}}{3{{a}^{2}}+{{b}^{2}}-{{c}^{2}}} \right)}=1\Rightarrow \prod\limits_{sym}{\left( 3{{a}^{2}}-{{b}^{2}}+{{c}^{2}} \right)}=\prod\limits_{sym}{\left( 3{{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)}$$ Giả sử $P(a,b,c)=\prod\limits_{sym}{\left( 3{{a}^{2}}-{{b}^{2}}+{{c}^{2}} \right)}-\prod\limits_{sym}{\left( 3{{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)}$, ta thấy rằng đây là đa thức có bậc không quá 6 và hơn nữa $P(a,t,t)=P(a,t,-t)=P(t,b,t)=P(t,b,-t)=P(t,t,c)=P(t,-t,c)=0$ nên nó có thể phân tích thành nhân tử dạng $P(a,b,c)=\gamma (a-b)(b-c)(c-a)(a+b)(b+c)(c+a)$ với $\gamma $ là một số thực nào đó.

Vì tam giác $ABC$ không cân nên $(a-b)(b-c)(c-a)\ne 0$ và do đó, đẳng thức trên không thể xảy ra được. Vậy các đoạn thẳng $AX, BY, CZ$ không đồng quy.
Ta có đpcm.

Em ủng hộ tiếp 4 bài sau:

Bài 5.

Cho dãy số $({{u}_{n}})$ xác định bởi $\left\{ \begin{align}
& {{a}_{0}}={{a}_{1}}=1, \\
& {{a}_{n+1}}=\frac{(2n+3){{a}_{n}}+3n{{a}_{n-1}}}{n+3},n\ge 1. \\
\end{align} \right.$
Chứng minh rằng tất cả số hạng của dãy đều nguyên.

Bài 6.

Với mỗi số nguyên dương $n,$ gọi ${{a}_{n}}$ là tổng số lượng các chữ số của ${{2}^{n}}$ và ${{5}^{n}}$ khi viết trong hệ thập phân. Hãy tìm tất cả các số nguyên dương $m$ sao cho tồn tại một hoán vị của các số ${{a}_{1}},{{a}_{2}},{{a}_{3}},...,{{a}_{m}}$ mà tổng của $k$ số hạng đầu tiên trong dãy hoán vị đó không chia hết cho $k$ với mọi $k=2,3,...,m$.

Bài 7.

Cho các số nguyên tố ${{p}_{1}},{{p}_{2}},{{p}_{3}},...,{{p}_{k}}$ đôi một khác nhau và cho các số tự nhiên bất kì ${{n}_{1}},{{n}_{2}},{{n}_{3}},...,{{n}_{k}}$ đều lớn hơn 2. Chứng minh rằng số các cặp $(x,y)$ không có thứ tự, nguyên tố cùng nhau và thỏa mãn đẳng thức sau $${{x}^{7}}+{{y}^{7}}=p_{1}^{{{n}_{1}}}\cdot p_{2}^{{{n}_{2}}}\cdot p_{3}^{{{n}_{3}}}\cdot ...\cdot p_{k}^{{{n}_{k}}}$$ không vượt quá ${{2}^{k+1}}.$


Bài 8.

Xét số nguyên dương $n>2.$ Cho $n$ túi kẹo, mỗi túi có đúng 1 viên kẹo và hai người $A,B$ chơi một trò chơi như sau: Ở mỗi lượt chơi, người chơi chọn hai túi kẹo tùy ý có số kẹo nguyên tố cùng nhau rồi gộp chúng lại thành một túi kẹo. Người nào không thực hiện được thao tác này thì thua cuộc.
Biết rằng $A$ là người đi trước và hai người chơi lần lượt, hỏi ai là người có chiến lược để thắng trò chơi này?
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[namdung]

Nguyên văn bởi huynhcongbang

Bài 6.

Với mỗi số nguyên dương $n,$ gọi ${{a}_{n}}$ là tổng số lượng các chữ số của ${{2}^{n}}$ và ${{5}^{n}}$ khi viết trong hệ thập phân. Hãy tìm tất cả các số nguyên dương $m$ sao cho tồn tại một hoán vị của các số ${{a}_{1}},{{a}_{2}},{{a}_{3}},...,{{a}_{m}}$ mà tổng của $k$ số hạng đầu tiên trong dãy hoán vị đó không chia hết cho $k$ với mọi $k=2,3,...,m$.

Thầy không ủng hộ lắm cách ghép cơ học của hai bài toán không cùng bản chất như bài toán đề xuất của Lữ.

Thầy nghĩ bài này nên phát biểu là: Tìm tất cả các số nguyên dương n sao cho tồn tại một hoán vị của các số {2, 3, ..., n+1} sao cho tổng của k số hạng đầu tiên trong dãy đó không chia hết cho k với mọi k = 2, 3, ..., n.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[huynhcongbang]

Nguyên văn bởi namdung

Thầy không ủng hộ lắm cách ghép cơ học của hai bài toán không cùng bản chất như bài toán đề xuất của Lữ.

Thầy nghĩ bài này nên phát biểu là: Tìm tất cả các số nguyên dương n sao cho tồn tại một hoán vị của các số {2, 3, ..., n+1} sao cho tổng của k số hạng đầu tiên trong dãy đó không chia hết cho k với mọi k = 2, 3, ..., n.

Dạ, bài này em lấy nguyên gốc bài 1.2 trong cuốn sách của anh Lê Quang Nẫm đó thầy. Đúng là nếu để dưới dạng các số $2, 3, 4, ..., n+1$ thì sẽ thuần túy hơn nhưng cái ý: "số chữ số của $2^n$ và $5^n$ viết trong hệ thập phân là $n+1$" thì không phải ai cũng biết nên có gì giới thiệu cho mọi người cũng tốt ạ.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[huynhcongbang]

Mình xin nêu gợi ý cho các bài đã nêu lần trước:

Bài 5.

Cho dãy số $({{u}_{n}})$ xác định bởi $\left\{ \begin{align}
& {{a}_{0}}={{a}_{1}}=1, \\
& {{a}_{n+1}}=\frac{(2n+3){{a}_{n}}+3n{{a}_{n-1}}}{n+3},n\ge 1. \\
\end{align} \right.$
Chứng minh rằng tất cả số hạng của dãy đều nguyên.

Gợi ý.
Bằng quy nạp, chứng minh rằng $a_{n+2} = a_{n+1} + \sum_{k=1}^n a_k \cdot a_{n-k}$ hoặc $a_n = \sum_{k=0}^n C_n^k C_k$, trong đó $C_k$ là số Catalan thứ $k$.

Đây là một bài trong cuốn "Problem from the book" của Titu nhưng không có lời giải, mọi người có thể tham khảo lời giải đầy đủ (bằng tiếng Hungary) tại đây:
http://www.komal.hu/verseny/2000-03/A.h.shtml

Bài 6.

Với mỗi số nguyên dương $n,$ gọi ${{a}_{n}}$ là tổng số lượng các chữ số của ${{2}^{n}}$ và ${{5}^{n}}$ khi viết trong hệ thập phân. Hãy tìm tất cả các số nguyên dương $m$ sao cho tồn tại một hoán vị của các số ${{a}_{1}},{{a}_{2}},{{a}_{3}},...,{{a}_{m}}$ mà tổng của $k$ số hạng đầu tiên trong dãy hoán vị đó không chia hết cho $k$ với mọi $k=2,3,...,m$.

Gợi ý.
Như thầy Dũng gợi ý lần trước thì $a_n = n+1$ với mọi $n$, chứng minh dễ dàng bằng cách dùng logarit thập phân. Đến đây chỉ cần viết ra các trường hợp nhỏ là có thể đoán được rồi quy nạp bình thường.

Bài 7.

Cho các số nguyên tố ${{p}_{1}},{{p}_{2}},{{p}_{3}},...,{{p}_{k}}$ đôi một khác nhau và cho các số tự nhiên bất kì ${{n}_{1}},{{n}_{2}},{{n}_{3}},...,{{n}_{k}}$ đều lớn hơn 2. Chứng minh rằng số các cặp $(x,y)$ không có thứ tự, nguyên tố cùng nhau và thỏa mãn đẳng thức sau $${{x}^{7}}+{{y}^{7}}=p_{1}^{{{n}_{1}}}\cdot p_{2}^{{{n}_{2}}}\cdot p_{3}^{{{n}_{3}}}\cdot ...\cdot p_{k}^{{{n}_{k}}}$$ không vượt quá ${{2}^{k+1}}.$

Gợi ý.
Do $\gcd (x,y)=1$ nên ta chứng minh được rằng $\gcd(x+y, x^6-x^5y+x^4y^3-x^3y^4+x^2y^5+xy^6) \in \{1,7 \}$.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[ThangToan]

1. Cho 0 < a, b, c, d < 1 và abcd = (1-a)(1-b)(1-c)(1-d). Chứng minh rằng
$ (a+b+c+d) - (a+c)(b+d) \ge 1 $

Lời giải. Dùng phương pháp hình học.Dựng hình vuông $ABCD $ có cạnh bằng $1 $. Gọi $M, N, P, Q $ lần lượt là các điểm nằm trên các cạnh (không trùng với đỉnh) $AB, BC, CD, DA $ sao cho $AM=a, BN=b, CP=c, DQ=d $. Khi đó ta có:
$S(ABCD)=S(MNPQ)+S(AMQ)+S(BMN)+S(CNP)+S(DPQ) $
$ \Leftrightarrow 2S\left( {ABCD} \right) = 2S\left( {MNPQ} \right) + a\left( {1 - d} \right) + b\left( {1 - a} \right) + c\left( {1 - b} \right) + d\left( {1 - c} \right) $
$ \Leftrightarrow 2 = 2S\left( {MNPQ} \right) + a + b + c + d - \left( {a + c} \right)\left( {b + d} \right) $ (1).
Bây giờ ta sẽ chứng minh $2S(MNPQ)\le 1 $ (2). Chú ý cặp số $(a, c); (b,d) $ có vai trò như nhau.
TH1. Nếu $b\le \frac{1}{2}, d\ge \frac{1}{2} $ hoặc $d\le \frac{1}{2}, b\ge \frac{1}{2} $
Thật vậy, từ $N $ kẻ đường thẳng song song với $AB $ cắt $MP $ tại $N' $ và từ $Q $ kẻ đường thẳng song song với $AB $ cắt $MP $ tại $Q' $. Khi đó
$\[S\left( {MNPQ} \right) = S\left( {NMP} \right) + S\left( {QMP} \right) = \frac{1}{2}BC.NN' + \frac{1}{2}AD.QQ'\] $
$\[S\left( {MNPQ} \right) = \frac{1}{2}\left( {NN' + QQ'} \right) \le \frac{1}{2}AB = \frac{1}{2}\] $.
Do đó $(2) $ đúng suy ra $(1) $ đúng. Vậy bđt được chứng minh.
TH2. $min\{a, b, c, d\}\ge \frac{1}{2} $ thì từ giả thiết ta có ngay $a=b=c=d=\frac{1}{2} $
Th3. $min\{b, d\}\ge \frac{1}{2}, max\{a, c\}\le \frac{1}{2} $
$\[a + b + c + d - \left( {a + c} \right)\left( {b + d} \right) \ge 1 \Leftrightarrow \left( {a + c - 1} \right)\left( {b + d - 1} \right) \le 0\] $ luôn đúng.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[12121993]

1. Cho 0 < a, b, c, d < 1 và abcd = (1-a)(1-b)(1-c)(1-d). Chứng minh rằng
$ (a+b+c+d) - (a+c)(b+d) \ge 1 $

Giải:
đpcm tương đương với $(a+c - 1)(b+d - 1) \le 0 $
Từ đẳng thức $abcd = (1-a)(1-b)(1-c)(1-d) $ không mất tính tổng quát, giả sử
$ac \le (1-a)(1-c) $ và $bd \ge (1-b)(1-d) $
Khai triển và thu gọn ta được $a+c - 1 \le 0 $ và $b+d - 1 \ge 0 $
Từ đó ta có bdt cần chứng minh. Đẳng thức xảy ra khi và chỉ khi $a+c = b+d =1 $.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[kien10a1]

Em góp một bài nhỏ:
Bài 9: Cho tam giác $ABC $ nhọn nội tiếp đường tròn $(O) $ với các đường cao $BE,CF $ và trực tâm $H $. $AO $ cắt $BC $ tại $K $, đường thẳng chứa trung tuyến của tam giác $HEF $ tại $H $ cắt $BC $ tại $L $. Chứng minh rằng: $K,L,E,F $ cùng thuộc một đường tròn.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[hien123]

Nguyên văn bởi kien10a1

Em góp một bài nhỏ:
Bài 9: Cho tam giác $ABC $ nhọn nội tiếp đường tròn $(O) $ với các đường cao $BE,CF $ và trực tâm $H $. $AO $ cắt $BC $ tại $K $, đường thẳng chứa trung tuyến của tam giác $HEF $ tại $H $ cắt $BC $ tại $L $. Chứng minh rằng: $K,L,E,F $ cùng thuộc một đường tròn.

Gọi M, N theo thứ tự là trung điểm của $BC$ và $EF$, đặt $P=AH\cap EF,Q=AO\cap (O),Q\neq A$. Dễ thấy, hai tam giác $ABC$ và $AEF$ đồng dạng nên $PK\parallel HQ$. Từ đó với chú ý, $H,M,Q$ thẳng hàng, suy ra $HM\parallel PK$. Do đó, $\widehat{HMB}=\widehat{PKL}$.
Mặt khác, từ hai tam giác $HEF$và $HBC$ đồng dạng, ta có $\widehat{HMB}=\widehat{HNF}$. Suy ra, $\widehat{PKL}=\widehat{PNL}$ hay tứ giác $PNKL$ nội tiếp. Bây giờ, gọi $T$ là giao điểm của $EF$ và $BC$. Khi đó, theo hệ thức Maclaurin và phương tích ta có $$\overline{TF}.\overline{TE}=\overline{TP}. \overline{TN}= \overline{TL}.\overline{TK}$$ Như vậy, bốn điểm $E,F,L,K$ cùng thuộc một đường tròn.
Bài 15. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, phân giác trong $AD$ ($D$ nằm trên cạnh $BC$). Một điểm $P$ di động trên đường phân giác trong $AD$ của tam giác $ABC$. Đường thẳng $BP$ cắt cạnh $AC$ tại điểm $E$, đường thẳng $CP$ cắt cạnh $AB$ tại điểm $F$. Gọi $M$ là hình chiếu của điểm $P$ trên đường thẳng $BC$. $PM$ cắt $EF$ tại $N$ và $AN$ cắt $OP$ tại $L$. Chứng minh $ML$ luôn đi qua một điểm cố định khi $P$ di động
Đây là bài toán cũ, đã có lời giải trên MS nhưng lời giải này chưa thực sự đơn giản và mang hơi hướng tính toán.
Bài 16. Cho đường tròn $(O_{1})$ và $(O_{2})$ cố định. Điểm $M$ di chuyển trên $(O_{1})$, đường kính $AB$ của $(O_{2})$ song song với $O_{1}M$. Đường thẳng $MA,MB$ theo thứ tự cắt $(O_{2})$ tại điểm thứ hai $C,D$. Chứng minh rằng $CD$ luôn đi qua một điểm cố định.
Lưu ý, khi giải 2 bài toán trên các bạn cần trình bày rõ cách dự đoán chính xác điểm cố định đồng thời trong quá trình giải không sử dụng máy tính!
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[12121993]

Nguyên văn bởi kien10a1

Em góp một bài nhỏ:
Bài 9: Cho tam giác $ABC $ nhọn nội tiếp đường tròn $(O) $ với các đường cao $BE,CF $ và trực tâm $H $. $AO $ cắt $BC $ tại $K $, đường thẳng chứa trung tuyến của tam giác $HEF $ tại $H $ cắt $BC $ tại $L $. Chứng minh rằng: $K,L,E,F $ cùng thuộc một đường tròn.

Một lời giải khác cho bài này.
Đặt $S = EF \cap BC , D = AH \cap BC , N = AH \cap EF $. $I $ là trung điểm của $EF $. Ta có $L, I, H $ thẳng hàng.
Ta có $(SNEF) = (SDCB) = -1 $ suy ra $\frac{\bar{SE}}{\bar{SF}} : \frac{\bar{NE}}{\bar{NF}} = -1 $ hay $\frac{\bar{SE}}{\bar{SF}} = - \frac{\bar{NE}}{\bar{NF}} $
Dễ thấy các tam giác $AEF $ và $ABC $ đồng dạng và $\widehat{NAE} =\widehat{KAB} $ nên ta có $\frac{\bar{NE}}{\bar{NF}} = \frac{\bar{KB}}{\bar{KC}} $.
Từ đó chú ý đến nhận xét ở trên ta có $\frac{\bar{SE}}{\bar{SF}} = - \frac{\bar{KB}}{\bar{KC}} $
Đặt $\frac{\bar{KB}}{\bar{KC}}=k; \frac{\bar{LB}}{\bar{LC}}=l $
Xét phép chiếu xuyên tâm $H $ ta có
$(SLBC) = (SIEF) $. Suy ra $\frac{\bar{SB}}{\bar{SC}} : \frac{\bar{LB}}{\bar{LC}} = \frac{\bar{SE}}{\bar{SF}} : \frac{\bar{IE}}{\bar{IF}} $.
Chú ý đến các đẳng thức ở trên và I là trung điểm EF, ta có $\bar{SB}=kl \bar{SC} $.
Ta sẽ chứng minh $\bar{SK} . \bar {SL} = \bar{SB} . \bar {SC} $
Điều này tương đương với
$ \frac{\bar{SB} - k \bar{SC}}{1-k} . \frac{\bar{SB} - l \bar{SC}}{1-l} = \bar{SB} . \bar {SC} $
Rút gọn ta có $\bar{SB}^2 - (1+kl)\bar{SB} . \bar {SC} + kl \bar{SC}^2 = 0 $
hay $(\bar{SB} - \bar{SC})(\bar{SB} - kl \bar{SC}) = 0 $
Điều này luôn đúng do $\bar{SB}=kl \bar{SC} $.
Chú ý rằng $BCEF $ nội tiếp nên ta có $\bar{SK} . \bar {SL} = \bar{SB} . \bar {SC} = \bar{SE} . \bar {SF} $.
Suy ra $E, F, K, L $ đồng viên.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[namdung]

Sau hơn 1 tuần nghỉ Tết, chúng ta lại trở lại với chương trình luyện thi TST. Theo thông báo từ BGD thì năm nay kỳ TST sẽ được tổ chức khá sớm, vào ngày 20/3. Như vậy là chỉ còn 1 tháng để các sĩ tử ôn luyện.

Hiện nay vẫn còn bài tập số 4 của chúng ta chưa có lời giải. Tôi bổ sung thêm một số bài mới.

Bài 17. Cho số nguyên dương n. Họ P các đoạn thẳng I = [i, j] với $0 \ge i < j \ge n $ được gọi là hạnh phúc nếu với hai đoạn I, J bất kỳ thuộc P, nếu I thuộc J thì ít nhất có một trong hai đầu mút của I trùng với một trong hai đầu mút của J. Tìm số đoạn thẳng lớn nhất của một họ hạnh phúc.

Bài 18. Ban đầu các ô của bảng vuông 5x5 được điền các số 0. Mỗi một lần thực hiện, cho phép tăng số được viết ở một ô bất kỳ và tất cả các ô có cạnh kề với ô đó lên 1 đơn vị. Hỏi có thể sau một số hữu hạn lần thực hiện thu được 1 bảng gồm toàn các số 2012?

Bài 19. Gọi $x_1 < x_2 < x_3 $ là ba nghiệm của phương trình $x^3 - 3x - 1 = 0 $. Chứng minh rằng
$x_3^2 - x_2^2 = x_3 - x_1 $
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[thiendienduong]

Nguyên văn bởi namdung

Bài 19. Gọi $x_1 < x_2 < x_3 $ là ba nghiệm của phương trình $x^3 - 3x - 1 = 0 $. Chứng minh rằng
$x_3^2 - x_2^2 = x_3 - x_1 $

Trước tiên ta đi tìm nghiệm bằng cách đặt $x=2\cos t$, $t\in \left [ 0;\pi \right ]$.
Dựa vào tính chất có tối đa $3$ nghiệm của phương trình bậc ba, ta tìm được $3$ nghiệm là:
$x_1=2\cos \frac{7\pi}{9}, x_2=2\cos \frac{5\pi}{9}, x_3=2\cos \frac{\pi}{9}$
Việc chứng minh đẳng thức ta dùng các công thức lượng giác trong sách giáo khoa.
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[NhamNgaHanh]

Anh ấy nói đúng rồi đấy Lữ ạ!
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[Traum]

Bài 10: Cho $a_1,a_2,...a_{63} $ là một hoán vị của $1,2,...,63 $. Chứng minh rằng có không quá 38 số chính phương xuất hiện trong dãy: $b_k = 2017 - a_1-\cdots -a_k $, $k = 1,2,...,63 $. (Độ khó = nằm giữa bài 1 và bài 2 theo kiểu IMO hay TST)

Bài 11: Tìm tất cả hàm số $f:Q^+\to Q^+ $ thỏa mãn: $f(2) = 2 $, $f(xy) = f(x)f(y) $ và $f(x+y)\le 4f(x) + 2013f(y) $ với mọi $x,y\in Q^+ $. (Độ khó = bài 2 IMO hay TST).
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT] 

[nqt]

Nguyên văn bởi Traum

Bài 11: Tìm tất cả hàm số $f:Q^+\to Q^+ $ thỏa mãn: $f(2) = 2 $, $f(xy) = f(x)f(y) $ và $f(x+y)\le 4f(x) + 2013f(y) $ với mọi $x,y\in Q^+ $. (Độ khó = bài 2 IMO hay TST).

$Q^{+}$ có chứa 0 không hèn?
[RIGHT][I][B]Nguồn: MathScope.ORG[/B][/I][/RIGHT]