


 |  | |  |
| |
| ||||||
 |
Ngoài một số quy định đã được nêu trong phần Quy định của Ghi Danh , mọi người tranh thủ bỏ ra 5 phút để đọc thêm một số Quy định sau để khỏi bị treo nick ở MathScope nhé ! * Quy định về việc viết bài trong diễn đàn MathScope * Nếu bạn muốn gia nhập đội ngũ BQT thì vui lòng tham gia tại đây |
  |
| | Ðiều Chỉnh | Xếp Bài |
| | #31 |
| +Thành Viên Danh Dự+  Tham gia ngày: Dec 2007 Bài gởi: 252 Thanks: 40 Thanked 455 Times in 95 Posts | Bài 6 hệ quả trực tiếp từ định lý Bondy  . Đầu tiên chọn ra 40 hs ta được 1 chu trình Hamiton. Chia 2 trường hợp: 2 hs còn lại quen nhau => xong. Nếu không quen thì 40 hs đó hợp hai hs thừa lập thành chu trình Hamiton. . Đầu tiên chọn ra 40 hs ta được 1 chu trình Hamiton. Chia 2 trường hợp: 2 hs còn lại quen nhau => xong. Nếu không quen thì 40 hs đó hợp hai hs thừa lập thành chu trình Hamiton.   Bài 3 khá hay, không bạn nào quan tâm à? |
| |  |
| | #32 |
| +Thành Viên+  Tham gia ngày: Jan 2012 Đến từ: ĐHSP Hà Nội, nhưng sau này sẽ là CHV Bài gởi: 15 Thanks: 0 Thanked 6 Times in 6 Posts | Bài này mình làm nhưng theo hướng khá đơn giản và ngắn nên ko ro đúng ko,bạn có thế post lời giải lên đc không? Xét $ax+by+cz+d\equiv 0 $( mod p) $\Leftrightarrow (y-x)b+(z-x)c\equiv -d $(mod p) $ \Leftrightarrow mb+cn\equiv -d $ (mod p)$m,n\in \left \{ \left \lfloor \frac{p}{3}-1,..1-\left \lfloor \frac{p}{3} \right \rfloor \right \rfloor \right \} $ $b^{-1}bm+ncb^{-1}\equiv db^{-1} $(mod p) $nx\equiv y-m $ (mod p) $nx\equiv t $(mod p) Trong đó n,ttnhận $2\left \lfloor \frac{p}{3} \right \rfloor-1 $ giá trị mà $2(2\left \lfloor \frac{p}{3} \right \rfloor-1)>p $ với p>17 nên dễ chọn được n,z thỏa mãn vậy t=3 thỏa mãn, với t>3 ta chọn a,b,c,d hoặc làm tiếp theo hướng kia hình như cũng được Một số chỗ hơi tắt các bạn thông cảm! __________________ 첸옥 H thay đổi nội dung bởi: VengefulSpirit, 18-04-2012 lúc 06:09 PM |
| |  |
| | #33 |
| +Thành Viên+  Tham gia ngày: Nov 2010 Bài gởi: 9 Thanks: 12 Thanked 1 Time in 1 Post | Mr Stoke là thầy đấy bạn ơi! |
| |  |
| | #34 | |
| Administrator   | Trích:
Bài này đúng là có liên quan đến các định lý Dirac, Ore, Bondy-Chvatal nhưng phải xem kỹ lại các chứng minh để xử lý việc "thiếu 1 chút". | |
| |  |
| | #35 |
| +Thành Viên+  Tham gia ngày: May 2009 Bài gởi: 20 Thanks: 30 Thanked 36 Times in 13 Posts | Vậy bài này nếu xét trường hợp có hai thành phần liên thông thì suy ra mỗi thành phần liên thông là K21 đầy đủ, còn nếu G liên thông thì chứng minh có chu trình Hamilton, hướng đi vậy đúng ko thầy? |
| |  |
| | #36 | |
| +Thành Viên+  Tham gia ngày: Jan 2012 Đến từ: Khu Rồng Thiên Bài gởi: 10 Thanks: 0 Thanked 10 Times in 3 Posts | Trích:
 __________________ | |
| |  |
| | #37 | |
| Administrator   | Trích:
------------------------------ Có lẽ đây là hướng đi đúng. thay đổi nội dung bởi: namdung, 18-04-2012 lúc 05:23 PM Lý do: Tự động gộp bài | |
| |  |
| | #38 |
| +Thành Viên+  Tham gia ngày: Dec 2009 Đến từ: HCM City Bài gởi: 183 Thanks: 25 Thanked 240 Times in 122 Posts | Bài 3 em có lời giải như sau: *Cho $b=c=1, a=p-2 $. Ta có: $ax+by+cz \equiv y+z-2x $ phải lập thành một hệ thặng dư đầy đủ mod p. Mà $-2([\frac{p}{t}]-1) \leq y+z-2x \leq 2([\frac{p}{t}]-1) $ nên ta có $4[\frac{p}{t}]+1 \geq p+1 \Rightarrow [\frac{p}{t}] \geq \frac{p}{4} \Rightarrow t<4 $. *Với $t=3 $: Ta sẽ chứng minh $ax+by+cz $ có thể nhận bất kì số dư nào khi chia cho p. $ax+by+cz \equiv b(y-x)+c(z-x) (mod p) $. Gọi $x_0, y_0, gcd(x_0,y_0)=1 $ thỏa $x_0b \equiv y_0c $, chứng minh được $(x_0,y_0) $ tồn tại duy nhất. Và $x_1b+y_1c \equiv x_2b+y_2c \Leftrightarrow x_1-x_2=tx_0, y_2-y_1}=ty_0 $. Khi đó, số cặp $(x_1,y_1), (x_2,y_2) $ thỏa điều trên là nhiều nhất khi $x_0=y_0=1 $, tức là số các số đồng dư nhau theo mod p trong tập $mb+nc $ là nhiều nhất, hay các số dư phân biệt khi chia cho p của tập là $mb+nc $ là ít nhất (chú ý rằng số phần tử của tập $b(y-x)+c(z-x) $ là không đổi khi b,c thay đổi (x,y,z thuộc ${0;1;...;[\frac{p}{t}]-1 $) ) khi $x_0=y_0=1 $. Ta chứng minh rằng khi đó, tập $ax+by+cz $ vẫn có thể lập thành hệ thặng dư đầy đủ mod p. Thật vậy: Trong trường hợp đó $ax+by+cz \equiv b(y+z-2x) (mod p) $. Chú ý rằng $gcd(b,p)=1, -2([\frac{p}{t}]-1) \leq y+z-2x \leq 2([\frac{p}{t}]-1) $ và $[-2([\frac{p}{t}]-1); 2([\frac{p}{t}]-1) ] $ chứa nhiều hơn p số nguyên khi $p>9 $, ta có điều cần chứng minh. |
| |  |
| The Following 2 Users Say Thank You to pth_tdn For This Useful Post: | gomis (22-04-2012), huynhcongbang (20-04-2012) |
| | #39 | |
| Administrator   Tham gia ngày: Mar 2009 Bài gởi: 349 Thanks: 0 Thanked 308 Times in 161 Posts | Trích:
thay đổi nội dung bởi: chemthan, 18-04-2012 lúc 07:05 PM | |
| |  |
| The Following User Says Thank You to chemthan For This Useful Post: | huynhcongbang (20-04-2012) |
| | #40 |
| +Thành Viên+  Tham gia ngày: Jan 2012 Đến từ: ĐHSP Hà Nội, nhưng sau này sẽ là CHV Bài gởi: 15 Thanks: 0 Thanked 6 Times in 6 Posts | Chắc bạn nói đến Đl Cauchz-Davenport nhưng định lý này cao cấp va phải động chạm đên Zp nên không hay lắm. __________________ 첸옥 H |
| |  |
| The Following User Says Thank You to VengefulSpirit For This Useful Post: | gomis (22-04-2012) |
| | #41 |
| Administrator   Tham gia ngày: Mar 2009 Bài gởi: 349 Thanks: 0 Thanked 308 Times in 161 Posts | |
| |  |
| | #42 |
| +Thành Viên+  Tham gia ngày: Jan 2012 Đến từ: THPT chuyên Lý Tự Trọng Cần Thơ Bài gởi: 4 Thanks: 0 Thanked 3 Times in 1 Post | 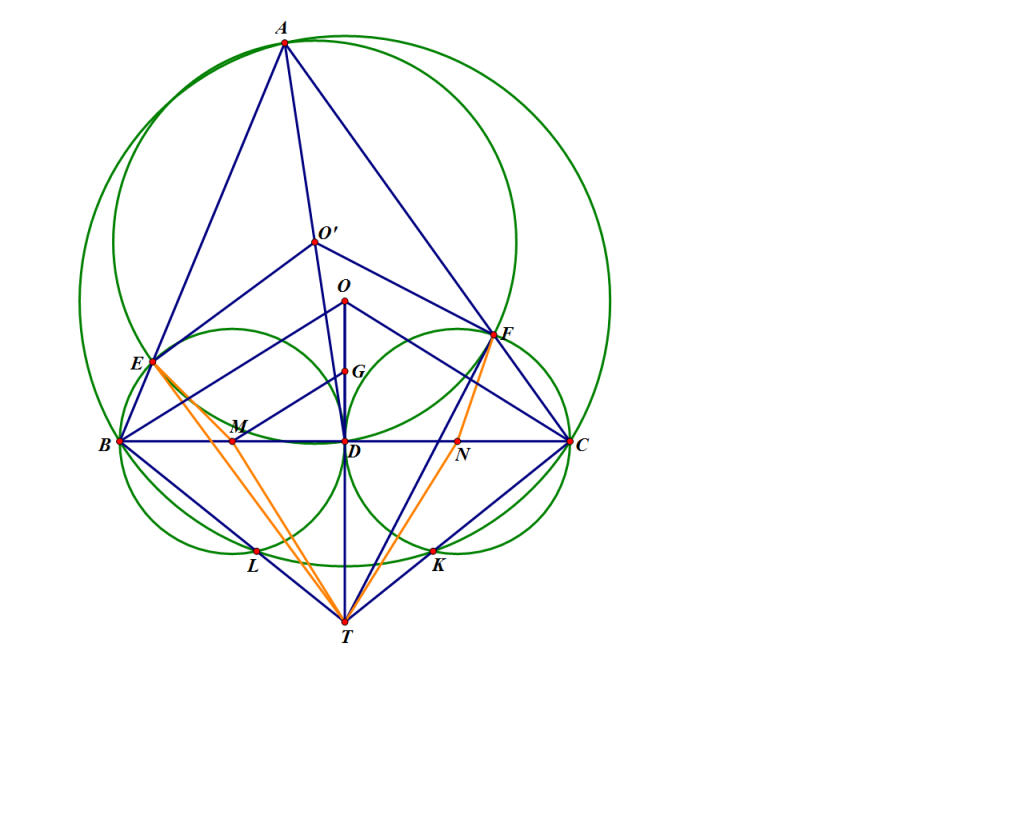 Cách giải khác cho bài 1: Xét bổ đề: Trên đường tròn (O) cho dây cung BC và một điểm A di động trên (O). Gọi D là trung điểm BC, đường tròn (O') đường kính AD cắt cạnh AB, AC tại E,F. Tiếp tuyến của (O') tại E, F cắt nhau tại T. Chứng minh T cố định. Chứng minh Gọi M, N là trung điểm BD, DC; ta có đường tròn đường kính BD đi qua E và đường tròn đường kính CD đi qua F. Ta có \[\widehat{MET} = \widehat{MEB} - ({180^0} - \widehat{AET}) = \widehat{MBE} + \widehat{AET} - {180^0}\] tương tự \[\widehat{NET} = {180^0} - \widehat{AFT} - \widehat{NCF}\] ta lại có: \[\widehat{MBE} + \widehat{AET} - {180^0} = {180^0} - \widehat{AFT} - \widehat{NCF}\] hay \[\widehat{AET} + \widehat{AFT} + 180 - \widehat{BAC} = 360\] hay \[\widehat{AET} - \widehat{O'EA} + \widehat{AFT} - \widehat{O'FA} = 180\] (đúng do tứ giác O'ETF nội tiếp) suy ra \[\widehat{MET} = \widehat{NET}\] Suy ra tam giác MET= tam giác NET Suy ra TM=TN => TD vuông góc với BC Ta lại có $P_{T/(M)}=TB^2-DB^2$ ; $P_{T/(O)}=TO^2-BO^2$ Như vậy nếu ta chúng minh đc $P_{T/(M)}=P_{T/(O)}$ Thì ta có thể kết luận rằng T là giao của trung trực BC và trục đẳng phương của (O) và (M), và do đó T cố định. Ta chứng minh cho $P_{T/(M)}=P_{T/(O)}$ (1) , thật vậy: (1) <=> $TO^2-BO^2=TB^2-DB^2$ <=> $TO^2-TB^2=BO^2-DB^2$ <=> $TO^2=OD^2+TB^2$ <=> $(OD+DT)^2=OD^2+DT^2+DB^2$ <=> $DB^2=2DO.DT$ (2) Gọi G là trung điểm của OD thì (2) <=> $DG.DT=DM^2$ <=> tam giác MGT vuông tại M <=> \[\widehat{MGD} + \widehat{MTD} = {90^0} < = > \widehat{BAC} + \frac{1}{2}\widehat{MTN} = {90^0}\] <=> \[\frac{1}{2}\widehat{EO'F} + \frac{1}{2}\widehat{ETF} = {90^0}\] (đúng) Áp dụng bổ đề trên cho tam giác HBC với H là trực tâm tam giác ABC và để ý rằng đường tròn ngoại tiếp tam giác HBC cố định, ta có đpcm thay đổi nội dung bởi: lethanhtu, 18-04-2012 lúc 10:22 PM |
| |  |
| The Following 3 Users Say Thank You to lethanhtu For This Useful Post: |
| | #43 | |
| Moderator  Tham gia ngày: Nov 2007 Đến từ: cyber world Bài gởi: 413 Thanks: 14 Thanked 466 Times in 171 Posts | Trích:
Ta có thể giải quyết như sau: Kí hiệu $S = \left\{0,1,...,\left[\frac{p}{3}\right]-1\right\} $ Trường hợp 1: 2 trong 3 số $a,b,c, $ bằng nhau theo mod p ( tất nhiên sẽ khác với số còn lại). Giả sử $a = b $ Ta có $ax+by+cz+d\equiv a(x+y)-2az +d \equiv a(x+y-2z) + d\pmod p $. Ta sẽ phải chứng minh tập $X = \{x+y-2z|x,y,z\in S\} $ là một hệ thặng dư đầy đủ mod p. (dễ chứng minh) Trường hợp 2: 3 số $a,b,c $ khác nhau và khác 0 theo mod p Xét tập $A = \{0,a,b,c\} $ thì $|A| = 4 $. Theo định lý Cauchy-Davenport thì tập $S(A) = \{ax+by+cz|x,y,z\in S\} $ có ít nhất là $\min\{p,4\left\lfloor\frac{p}{3}\right\rfloor-3\} $ phần tử khác nhau theo mod p. Với $p\ge 17 $ thì $4\left\lfloor\frac{p}{3}\right\rfloor-3\ge p $ nên ta có S(A) là một hệ thặng dư đầy đủ mod p. Do đó với $t = 3 $ thì tồn tại $x,y,z $ thỏa mãn. Với $t = 4 $ thì cũng có thể chỉ ra được $a,b,c,d $ sao cho không tồn tại $x,y,z $ thỏa mãn ( ví dụ $a = b = 1, c = p-2 $ và $d = \frac{p+1}{2} $ __________________ Traum is giấc mơ. thay đổi nội dung bởi: Traum, 18-04-2012 lúc 09:10 PM | |
| |  |
| The Following User Says Thank You to Traum For This Useful Post: | huynhcongbang (20-04-2012) |
| | #44 | ||
| +Thành Viên+  Tham gia ngày: Nov 2011 Bài gởi: 6 Thanks: 1 Thanked 1 Time in 1 Post | Trích:
Trích:
| ||
| |  |
| The Following User Says Thank You to Làng Sình For This Useful Post: | huynhcongbang (20-04-2012) |
| | #45 | |
| Moderator  Tham gia ngày: Nov 2007 Đến từ: cyber world Bài gởi: 413 Thanks: 14 Thanked 466 Times in 171 Posts | Trích:
Một hướng khác là sử dụng định lý Tutte cho đồ thị có perfect matching. Chú ý: Lời giải cho bài toán trong cuộc thi chắc chắn sẽ đơn giản hơn rất nhiều so với ở đây!!! Trường hợp 1: Đồ thị không liên thông Có ít nhất là 2 thành phần liên thông rời nhau, do bậc mỗi đỉnh là 20 nên chỉ có duy nhất một đồ thị thỏa mãn là hợp của 2 $K_{21} $ rời nhau. Trường hợp 2: Đồ thị liên thông Xem [Only registered and activated users can see links. ], cho các định nghĩa và kí hiệu. Giả sử không có perfect matching, khi đó theo định lý Tutte tồn tại một tập các đỉnh $U $ sao cho $odd(G-U)>|U| $. Đặt $|U| = k $ và $odd(G-U) = q $, gọi các thành phần liên thông có lẻ đỉnh đó là $A_{1},...,A_{q} $. Tổng số đỉnh trong đồ thị là $42 \equiv |A_{1}|+...+|A_{q}| + |U| \pmod 2 $. Do $|A_{i}| $ lẻ nên ta có $q + k \equiv 0 \pmod 2 $. Ở trên ta giả sử $q>k $ nên $q\ge k+2 $. Gọi $t_i $ là số cạch có một đầu thuộc $U $ và một đầu thuộc $A_{i} $. Do đồ thị liên thông nên $t_i\ge 1 $. Tổng số bậc của các đỉnh nằm trong $U $ là $20k\ge\sum\limits_{i=1}^{q}t_i $. Vì $q\ge k+2 $ nên phải có ít nhất là 3 chỉ số $i $ sao cho $t_i<20 $. Giả sử $t_1,t_2,t_3 \le 19 $. Do bậc mỗi đỉnh là 20 nên ta có $|A_1|,|A_2|,|A_3| >1 $ và do chúng lẻ nên $\ge 3 $. Do $|A_1|+|A_2|+|A_3|\le 42-k $ nên ta có giả sử $|A_1|\le 13 $ Đặt $a = |A_1|\le 13 $. Tổng số bậc của các đỉnh trong $A_1 $ không quá $a(a-1) + t_1 $, mà mỗi đỉnh có bậc là 20 nên $a(a-1)+t_1\ge 20a $. Ở trên ta có $t_1\le 19 $ nên $a(a-1)+20>20a $ do đó $a(a-1)>20(a-1) $ hay $a>20 $ mâu thuẫn. __________________ Traum is giấc mơ. | |
| |  |
| The Following 3 Users Say Thank You to Traum For This Useful Post: |
   |
| Bookmarks |
|
|